
A guide for self-directed investors who want to optimize their portfolio performance
Diversification is a key concept in investing that can help you reduce your exposure to market fluctuations and improve your long-term returns. But what does diversification mean and how can you apply it to your own portfolio? In this blog post, we will explain the basics of diversification using two perspectives: statistics (standard deviation) and finance (modern portfolio theory). We will also provide some examples of how diversification works in practice and why it is especially important for self-directed investors who make their own investment decisions.
Statistics: Standard Deviation And Correlation
Standard deviation is a measure of how much a set of values varies from the average. The higher the standard deviation, the more unpredictable the returns are and the more likely they are to deviate from the expected value. The lower the standard deviation, the more stable and consistent the returns are and the closer they are to the average. In investing, standard deviation is expressed in terms of volatility or risk of an asset or a portfolio. For example, let’s say you have two stocks, A and B, that have the same expected return of 10% per year, but different standard deviations. Stock A has a standard deviation of 20%, which means that its annual returns can range from -10% to 30%. Stock B has a standard deviation of 10%, which means that its annual returns can range from 0% to 20%. Which stock is riskier? Stock A, because it has a higher chance of losing money or underperforming the average. Which stock is more predictable? Stock B, because it has a lower chance of deviating from the expected return.
To go from standard deviation of individual assets to standard deviation of combined assets, we must understand their correlation. Correlation is a statistical measure that indicates how two assets move in relation to each other. A correlation coefficient, which ranges between -1 and +1, is used to express this relationship. A correlation of +1 means that the assets are perfectly correlated and move in unison—there is no diversification benefits between the two assets. A correlation of -1 means that they move in opposite directions—the combination of the two assets has no risk at all. Finally, a correlation of 0 suggests there is no relationship in their movements. Correlation is measured as a coefficient. In our stock example, let’s say that the correlation coefficient between Stock A and stock B is .5, meaning the stocks are positive but not perfectly correlated.
Diversification is a risk management strategy that mixes a wide variety of investments within a portfolio. The rationale behind this technique is that a portfolio constructed of different kinds of investments will, on average, yield higher returns and pose a lower risk than any individual investment within the portfolio. This shows that by combining two risky assets, you can reduce the overall risk of your portfolio, as long as the assets are not perfectly positively correlated. This is the essence of diversification: by spreading your money across different assets that have different risk-return profiles and different correlations, you can lower your portfolio volatility and increase your chances of achieving your expected return. Let’s continue with our example of stock A and stock B, but to get a better understanding of this process, wee need to see the math behind it. Portfolio standard deviation is expressed mathematically as follows:
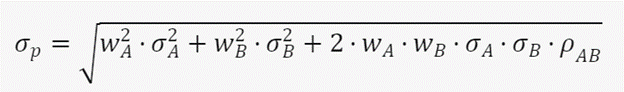
where:
- σp is the standard deviation of the portfolio,
- WA and WB are the weights of the assets in the portfolio,
- σA and σB are the standard deviations of the returns of the assets,
- ρAB is the correlation coefficient between the returns of the assets.
Continuing our stock A and B example, here is the same formula with the corresponding numbers:
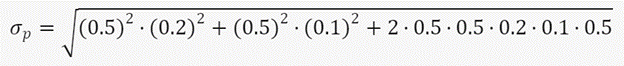
This equals a portfolio standard deviation of approximately 0.1323 or 13.23%. When compared with the average taken from both standard deviations (15%), the addition of both stocks together actually reduces the new joint portfolio standard deviation. This highlights that by combining two risky assets, you can reduce the overall risk of your portfolio, as long as the assets are not perfectly positively correlated. This is the essence of diversification: by spreading your money across different assets that have different risk-return profiles and different correlations, you can lower your portfolio volatility and increase your chances of achieving your expected return. This is further expanded on in the concept of modern portfolio theory.
Finance: Modern Portfolio Theory
Modern portfolio theory (MPT) is a framework for building optimal portfolios that maximize expected return for a given level of risk, or minimize risk for a given level of expected return. MPT is based on the idea that investors are rational and risk-averse, meaning that they prefer higher returns and lower risks, and that they can diversify away the unsystematic risk or the specific risk of individual assets by holding a large number of assets in their portfolio.
MPT uses the formulas previously discussed for standard deviation and correlation, as well as a calculation for returns. Based on these calculations, MPT can generate a set of optimal portfolios that offer the best trade-off between risk and return. MPT also identifies the optimal portfolio for each investor, depending on their risk tolerance and return preference, which is the portfolio that gives them the highest satisfaction or utility.
For example, let’s say you have three assets to choose from: a risk-free asset that has a return of 2% and a standard deviation of 0%, a low-risk asset that has a return of 6% and a standard deviation of 10%, and a high-risk asset that has a return of 12% and a standard deviation of 20%. You can create different portfolios by allocating different weights to these assets, and calculate their expected return and standard deviation using MPT formulas. You can also compare these portfolios based on their risk-return characteristics. Some of the possible portfolios are:
- A portfolio that consists of 100% of the risk-free asset, which has a return of 2% and a standard deviation of 0%. This portfolio has the lowest risk and return, and is suitable for investors who are very risk-averse and do not want to take any chances with their money.
- A portfolio that consists of 50% of the low-risk asset and 50% of the high-risk asset, which has a return of 9% and a standard deviation of 11.2%. This portfolio has a moderate risk and return, and is suitable for investors who are willing to take some risk for higher returns, but not too much.
- A portfolio that consists of 100% of the high-risk asset, which has a return of 12% and a standard deviation of 20%. This portfolio has the highest risk and return, and is suitable for investors who are very risk-tolerant and seek the highest possible returns, regardless of the volatility.
- A portfolio that consists of 20% of the risk-free asset, 40% of the low-risk asset, and 40% of the high-risk asset, which has a return of 8.4% and a standard deviation of 8.8%. This portfolio has a lower risk and a higher return than the portfolio that consists of 50% of the low-risk asset and 50% of the high-risk asset, and is the optimal portfolio for investors who prefer a return of 8.4%. This portfolio lies on the efficient frontier, which is the curve that shows the optimal portfolios that offer the highest return for each level of risk.
Notice that the optimal portfolios are not the individual assets, but rather a combination of them, which demonstrates the benefit of diversification.
MPT also introduces the concept of the market portfolio, which is the portfolio that contains all the available assets in the market, weighted by their market value. The market portfolio is the most diversified portfolio possible, and it lies on the efficient frontier. MPT assumes that the market portfolio is the optimal portfolio for all investors, and that any deviation from the market portfolio is due to the investor’s personal preference for risk or return. MPT also defines the capital asset pricing model (CAPM), which is a formula that relates the expected return of an asset to its systematic risk or its sensitivity to the market portfolio. CAPM can be used to estimate the fair or required return of an asset, given its risk and the risk-free rate.
Why Diversification Is Important for Self-Directed Investors
Diversification serves as an important strategy for self-directed investors aiming to optimize their portfolio performance and mitigate investment risk. By spreading investments across various asset classes, sectors, regions, and strategies, these investors can reap several benefits:
- Lowers portfolio volatility, smooths returns over time. This stability can help investors avoid emotional reactions to market fluctuations and stay focused on long-term goals.
- Exposure to unsystematic risk, or the specific risk tied to individual assets, can be reduced. Such risks could stem from company performance, industry trends, regulatory shifts, or geopolitical events.
- Exposure to systematic risk, or market risk that impacts all market assets, can be increased. This type of risk is typically rewarded with higher expected returns over the long run.
- Opportunities and benefits across different asset classes, sectors, regions, and strategies can be captured. These elements can have varying risk-return profiles and correlations and can perform differently under diverse market conditions.
- Portfolios can be aligned with the investor’s risk tolerance and return preference, enabling the identification of an optimal portfolio that maximizes investor satisfaction.
Conclusion
It’s important to note that diversification is not a guarantee against losses. Instead, it’s a method of managing risk and enhancing returns. A major con of diversification stems from the weakness in standard deviation: data is based on historical observations, but there is no law that the past must repeat. Diversification doesn’t eliminate the need for research, analysis, and due diligence; it complements these activities. Diversification doesn’t simply mean holding a large number of assets, but rather maintaining a balanced and diversified mix of assets. Diversification is not a one-time action; it’s a continuous process that necessitates regular monitoring, rebalancing, and adjustments.
RELATED POSTS
View all


